Neural Networks : Learning

Coursera에서 진행되는 Andrew Ng 교수님의 Machine Learning 강의를 수강한 후 정리한 내용입니다.

Cost Function

Neural Network의 cost function을 배우기 전에 Neural Network의 classification을 복습해보도록 하겠습니다.

먼저 Binary classification은 y의 output unit이 1개입니다.

또, output unit y가 가지는 값은 0 혹은 1입니다.

 

Multi-class classification은 output units이 k개, 즉 2개 이상입니다.

따라서, y가 k차원의 행렬이 됩니다.

 

이전 게시물 마지막 파트에서 공부했던 것과 같이 Multi-class classification은 output 행렬의 모든 행 중 단 하나의 행만 1의 값을 가지고 다른 행들은 모두 0의 값을 가집니다.

 

이전 게시물은 아래 링크를 참고해주세요.

https://dvpzeekke.tistory.com/6

Neural Networks : Representation

 

logistic regression과 Neural Network(이하 NN)은 logistic function을 사용한다는 공통점이 있습니다.

logistic function을 사용하는 이유는 output을 binary data로 만들기 위함입니다.

 

logistic function과 NN의 차이는 cost function에서 드러납니다.

먼저 둘의 cost function은 아래와 같습니다.

cost function에 사용되는 변수들을 먼저 설명해보겠습니다.

L은 network에서 사용되는 layer의 개수입니다.

sl은 l번째 layer에 속한 unit의 개수입니다.(이때, bias unit은 포함하지 않습니다.)

K는 output unit의 개수입니다.

 

NN의 cost function은 logistic function의 cost function에서 sigma연산이 3번 추가된 형태입니다.

첫번째로 추가된 sigma연산은 J(Θ)의 첫번째 항에서 볼 수 있습니다.

logistic regression와 달리 NN이 K개의 output unit을 가짐을 고려해 추가된 연산입니다.

두번째, 세번째로 추가된 sigma 연산은 J(Θ)의 마지막 항에서 볼 수 있습니다.

마지막 항에서 두 개의 sigma 연산이 추가된 이유는 Θ 행렬 때문입니다.

Θ는 layers 사이의 mapping에 관여하는 행렬이기 때문에 총 L-1개의 Θ행렬이 존재합니다.

각 Θ 행렬의 행 개수는 다음 layer의 unit 개수, 즉 s(l+1)개 입니다.

또, 각 Θ 행렬의 열 개수는 해당 layer의 unit 개수, 즉 sl개 입니다.

이와 같은 이유에 의해 cost function이 위처럼 정의됩니다.

 

Backpropagation Algorithm

cost function 파트에서 cost function J(Θ)를 정의했습니다.

cost function의 output이 작을 수록 output error가 작다는 것을 의미하기 때문에, cost function을 최소화하는 것이 중요합니다.

이를 최소화하는 방법은 적합한 parameter를 찾는 것 입니다.

최적의 parameter를 찾기 위해선 결론적으로 J(Θ)의 편미분 식을 계산해야합니다.

Forward propagation은 input layer에서 시작해 output node의 값을 구하는 과정인 반면,

Backpropagation(이하 BP)는 output layer에서 시작하고 output node의 error를 통해 이전 layer node들의 error를 찾는 과정입니다.

 

forward propagation의 과정은 위와 같습니다.

이전 게시물에서 충분히 공부한 내용이기 때문에 넘어가도록 하겠습니다.

 

BP 진행 과정에 대해 알아보겠습니다.

 

BP는 layer 간의 역방향순으로 과정이 진행됩니다.

델타는 특정 노드에서의 error를 의미합니다.

이 델타값은 J(Θ)의 편미분값을 계산하기 위해 사용됩니다.

 

먼저 output 노드의 델타값(output error)을 구하는 과정은 간단합니다.

계산된 결과인 a의 값에서 y값을 빼준 값입니다.

이전 layer의 델타값을 구하는 식은 아래와 같습니다.

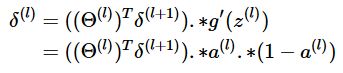
위 식에서 보시는 것 처럼 Θ의 역행렬과 sigmoid 함수의 미분값을 곱해 연산합니다.

sigmoid 함수의 미분값은 a(l)*(1-a(l))와 같기 때문에 이로 치환하는 것도 가능합니다.

 

training set이 m개일 때 BP 진행 과정을 살펴보겠습니다.

아래 그림을 참고해주세요.

대문자 델타값은 J(Θ)의 편미분 값을 구하기 위해 사용됩니다.

training set이 m개이기 때문에 m번의 for문을 돌게 됩니다.

먼저 input layer의 a값을 input값과 같게 설정합니다.

그 후 forward propagation을 진행합니다.

forward propagation 과정이 끝나면 BP를 시작합니다.

input layer를 제외한 모든 layer에 속한 unit의 델타값을 계산합니다.

그리고나서 현재 layer의 a값과 델타값을 곱해 J(Θ)의 편미분값을 계산합니다.

 

Backpropagation Instuition

BP의 이해를 돕기 위해 cost function의 정의를 제시합니다.

위 사진 속의 cost(i)가 cost function입니다.

정규화를 위해서 람다는 0으로 가정합니다.

 

 

델타값은 l*j개의 unit의 cost function으로 정의할 수 있습니다.

델타값은 cost function을 z에 대해 편미분한 값과 같습니다.

직관적으로 말하자면, 각 노드의 델타값은 cost function에 미치는 gradient라 할 수 있습니다.

때문에 델타값을 파악하면 Θ를 적절하게 조절할 수 있게됩니다.

 

Implementation Note: Unrolling Parameters

이 파트에서는 advanced optimization을 위해 파라미터를 unroll하는 법을 배웁니다.

옥타브로 실습할 때 필요한 내용이나, 저의 경우 실습은 생략했기 때문에 간단히 보고 넘어갔습니다.

생략하실 분들은 아래 Random Initialization 파트로 이동해주세요.

 

advanced optimization은 벡터 형태의 데이터를 필요로합니다.

하지만 NN에선 Θ, D와 같은 행렬 set을 사용하기 때문에 벡터형태로 unroll하는 과정이 필요합니다.

thetaVec은 Θ 행렬들을 모아서 만든 벡터이고, DVec은 D 행렬들을 모아서 만든 벡터입니다.

Theta1, 2, 3과 같이, thetaVec과 DVec에서 특정 행렬을 추출해낼 수도 있습니다.

 

Gradient checking

gradient checking은 기울기의 근사값을 구한 후 실제 기울기 값이랑 비교하는 것입니다.

training이 제대로 되고 있는지 확인하기 위해서 사용됩니다.

gradient checking을 cost function에 적용하면 위와 같습니다.

J(Θ)의 기울기에 대한 근사값(gradApprox)은 one side difference 혹은 two side difference 방법으로 계산할 수 있습니다.

더 정확한 결과를 가져오기 위해선 주로 two side difference를 사용합니다.

 

Θ별 기울기의 근사치(gradApprox)를 구하는 방법은 위와 같습니다.

two side difference를 사용하고 있습니다.

 

Random initialization

어떤 algorithm을 사용하던간에 초기 Θ값을 세팅해주는 과정이 필요합니다.

그렇다면 초기 Θ값을 어떤 값으로 설정하는 것이 적합한지 판단해야합니다.

logistic regression은 초기 Θ값을 모두 0으로 설정해도 아무 문제 없었지만 NN의 경우 문제가 발생합니다.

위 그래프에서 초기 Θ값을 모두 0으로 초기화했다 가정하고 얘기해보겠습니다.

먼저 forward propagation을 수행하면서 두번째 layer의 모든 unit의 a값이 동일해집니다.

그 다음, BP를 수행하면서 두번째 layer의 모든 unit의 델타값도 동일해집니다.

따라서, J(Θ)를 Θ로 편미분한 값도 각각 동일해집니다.

결과적으로 BP가 일어날 때 마다 첫번째 layer의 Θ값은 같은 값으로만 업데이트됩니다.

 

따라서, NN에서 zero initialization을 사용하면 다수의 뉴런을 보유하고 있는 장점에도 불구하고 중복 뉴런의 사용으로 비효율적인 결과가 나타납니다.

 

위와 같은 문제를 극복하기 위해서 random initialization을 사용합니다.

 

Putting it together

NN을 훈련하는데에 있어서 고려해야할 점은 network architecture 입니다.

network architecture를 설계할 때 고려할 점은 아래와 같습니다.

1. input unit의 개수

2. output unit의 개수

3. 모든 hidden layer안의 unit의 개수를 default 값으로 지정

 

다음은 NN을 훈련을 위한 순서입니다.

1. weight를 random initialize 한다.

2. 임의의 input을 대입해 h(x)를 구한다.

3. BP를 구현한다.

4. forward propagation, backpropagation을 반복한다.

5. J(Θ)를 Θ로 편미분한 값과 gradient checking으로부터 구한 근사치를 비교한다.

6. gradient descent나 advanced optimization 방법을 이용해 최적 parameter를 구한다.